Understanding Quick Sort: A Comprehensive Guide

Have you ever wondered how computers quickly arrange an unordered list of numbers or words with remarkable efficiency? The answer lies in an ingenious sorting algorithm known as "quick sort." This sorting method is renowned for its speed and efficiency, making it a favorite for software engineers and computer scientists worldwide. But what exactly is quick sort, and how does it work its magic? In this article, we will unravel the mysteries of quick sort, exploring its underlying principles, advantages, and practical applications.

Sorting algorithms are essential to computer science, allowing us to arrange data in an organized manner so that it can be easily accessed and analyzed. Among these algorithms, quick sort stands out for its performance and elegance. Developed by Tony Hoare in 1960, quick sort is a comparison sort that utilizes a divide-and-conquer strategy to sort elements efficiently. Whether it's organizing a list of names, numbers, or any other data type, quick sort offers a robust solution that balances speed and resource usage.

As we dive deeper into the workings of quick sort, we'll explore its algorithmic structure, understand its efficiency compared to other sorting techniques, and examine the real-world scenarios where it shines. Our journey will take us through the intricacies of partitioning, recursion, and optimization techniques, providing you with a thorough understanding of why quick sort remains a cornerstone in the realm of computer science. So, let's embark on this enlightening journey to decode the secrets of quick sort and appreciate its contributions to the digital world.

Read also:

Unbeatable Costco Korean Corn Dogs A Taste Of Seoul In Your Neighborhood

Table of Contents

• What is Quick Sort?
• Historical Background and Origin
• How Quick Sort Works
• The Partitioning Process
• The Recursive Nature of Quick Sort
• Time Complexity Analysis
• Advantages of Quick Sort
• Disadvantages and Limitations
• Quick Sort vs. Other Sorting Algorithms
• Applications of Quick Sort
• Implementing Quick Sort in Code
• Optimizing Quick Sort
• Common Misconceptions
• Frequently Asked Questions
• Conclusion

What is Quick Sort?

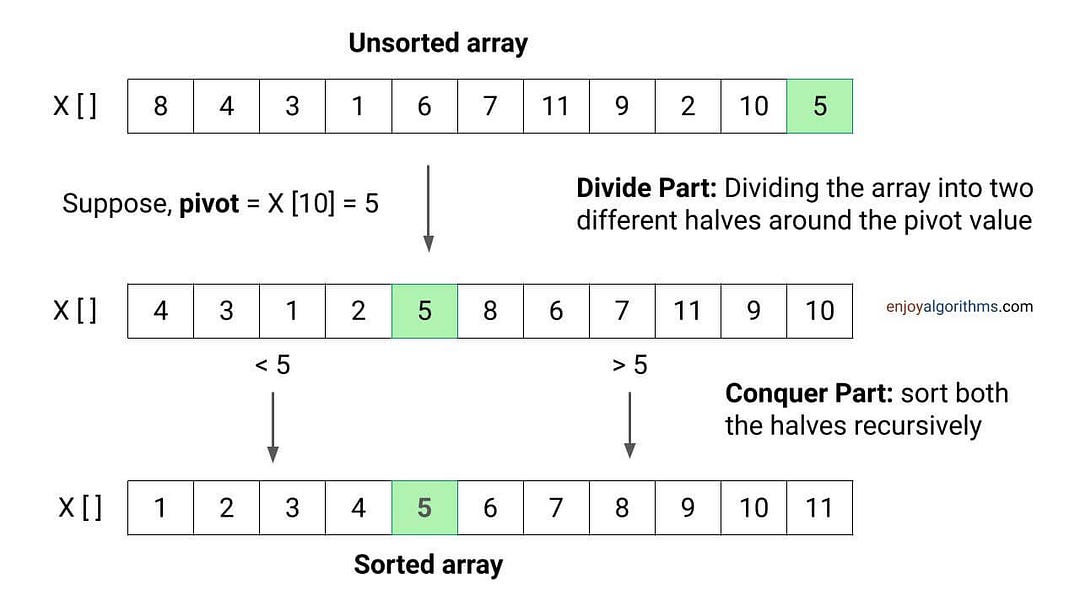
Quick sort is a highly efficient sorting algorithm that employs a divide-and-conquer approach to organize elements within a list or array. The core idea behind quick sort lies in partitioning the array into smaller sub-arrays based on a pivot element and then recursively sorting the sub-arrays. This process continues until the base case is reached, resulting in a sorted array.

The beauty of quick sort lies in its simplicity and adaptability. It can handle large datasets with ease, making it ideal for complex applications that require rapid data organization. Moreover, quick sort is an in-place sorting algorithm, meaning it requires minimal additional memory space, which is crucial for performance optimization in resource-constrained environments.

Despite its apparent simplicity, quick sort's efficiency largely depends on the choice of pivot and the strategy used to partition the array. In the following sections, we will delve deeper into the mechanics of quick sort, examining how these factors influence its performance and exploring the techniques used to optimize the algorithm for various scenarios.

Historical Background and Origin

The story of quick sort begins in the 1960s when Tony Hoare, a British computer scientist, introduced this revolutionary sorting algorithm. At the time, Hoare was working on a project related to machine translation and needed an efficient method to sort words. His innovation led to the creation of quick sort, which quickly gained recognition for its exceptional performance.

Quick sort's influence extends beyond its initial application, serving as a foundation for numerous advancements in computer science. Over the years, researchers and developers have refined and optimized the algorithm, enhancing its efficiency and applicability across various domains. Today, quick sort remains a vital component of sorting libraries and is widely taught in computer science curricula worldwide.

Understanding the historical context of quick sort provides valuable insights into its development and evolution. It highlights the algorithm's significance and underscores the importance of innovation in solving complex computational problems. As we continue our exploration of quick sort, we will uncover the principles that have made it a lasting solution in the world of sorting algorithms.

Read also:

The Tragic Demise Of Kurt Cobain Unraveling The Mystery

How Quick Sort Works

The quick sort algorithm is built on a simple yet powerful principle: partitioning the array into smaller parts and sorting them independently. The process can be divided into several key steps:

1. Choose a pivot element: The pivot is a crucial element in quick sort, as it determines how the array will be partitioned. The choice of pivot can significantly impact the algorithm's efficiency, and various strategies exist for selecting the pivot, such as choosing the first element, the last element, or a random element from the array.
2. Partition the array: The partitioning process involves rearranging the array so that elements smaller than the pivot are placed on the left, and elements larger than the pivot are placed on the right. This ensures that the pivot is in its correct position in the sorted array.
3. Recursively sort the sub-arrays: Once the array is partitioned, quick sort is applied recursively to the left and right sub-arrays. This process continues until the sub-arrays contain only one element or are empty, at which point they are considered sorted.

By following these steps, quick sort efficiently organizes the elements within the array, leveraging the divide-and-conquer strategy to achieve optimal performance. The algorithm's effectiveness is largely attributed to its ability to break down large problems into smaller, more manageable tasks, which can be solved independently.

The Partitioning Process

The partitioning process is a critical component of the quick sort algorithm, as it determines how the array is divided into smaller sub-arrays. During partitioning, elements are rearranged based on their comparison with the chosen pivot. The goal is to ensure that all elements smaller than the pivot are placed on its left, while those larger are on its right.

There are several methods for partitioning an array, with the most common being the Lomuto partitioning scheme and the Hoare partitioning scheme. Each method has its advantages and disadvantages, and the choice of partitioning scheme can affect the overall efficiency of the quick sort algorithm.

The Lomuto partitioning scheme involves iterating through the array and swapping elements to achieve the desired arrangement. In contrast, the Hoare partitioning scheme uses two pointers that converge toward each other, swapping elements when necessary. While both methods achieve the same result, their performance may vary depending on the specific characteristics of the input data.

The Recursive Nature of Quick Sort

Quick sort's recursive nature is a defining feature that contributes to its efficiency and elegance. By breaking down the sorting problem into smaller sub-problems, the algorithm can tackle each part independently, leading to faster overall sorting.

Recursion in quick sort involves calling the quick sort function on the left and right sub-arrays created during the partitioning process. This recursive process continues until the base case is reached, which occurs when the sub-arrays contain only one element or are empty. At this point, the sub-arrays are considered sorted, and the algorithm terminates.

While recursion is a powerful tool, it can also pose challenges, particularly in terms of memory usage and stack overflow risks. To mitigate these issues, developers may employ optimization techniques such as tail recursion and iterative implementations, which reduce the algorithm's reliance on the call stack and improve its overall performance.

Time Complexity Analysis

The time complexity of quick sort is an important consideration when evaluating its efficiency compared to other sorting algorithms. Quick sort's average-case time complexity is O(n log n), making it one of the fastest comparison-based sorting algorithms available.

However, quick sort's worst-case time complexity is O(n^2), which occurs when the pivot selection consistently results in highly unbalanced partitions. While this scenario is rare, it can significantly impact the algorithm's performance, particularly for large datasets.

To minimize the risk of encountering the worst-case time complexity, developers can employ strategies such as random pivot selection and median-of-three pivot selection, which improve the likelihood of achieving balanced partitions and maintaining the algorithm's average-case efficiency.

Advantages of Quick Sort

Quick sort offers several advantages that make it a popular choice for sorting applications:

• Efficiency: Quick sort's average-case time complexity of O(n log n) makes it one of the fastest sorting algorithms available, especially for large datasets.
• In-place sorting: Unlike some sorting algorithms that require additional memory space, quick sort is an in-place sorting algorithm, meaning it sorts the data within the original array without requiring extra storage.
• Flexibility: Quick sort can be easily adapted to different data types and applications, making it a versatile solution for various sorting tasks.
• Parallelization: Quick sort's divide-and-conquer strategy lends itself well to parallelization, allowing for further performance improvements on multi-core processors.

These advantages contribute to quick sort's widespread adoption and continued relevance in the field of computer science.

Disadvantages and Limitations

Despite its many advantages, quick sort is not without its limitations:

• Worst-case time complexity: Quick sort's worst-case time complexity of O(n^2) can be a concern for certain datasets, particularly if the pivot selection consistently results in unbalanced partitions.
• Recursive depth: The recursive nature of quick sort can lead to stack overflow issues for large datasets, particularly if the recursion depth is not managed carefully.
• Sensitivity to input order: Quick sort's performance can be affected by the initial order of the input data, with certain patterns potentially leading to suboptimal partitioning.

These limitations highlight the importance of understanding quick sort's behavior and carefully selecting strategies to optimize its performance for specific use cases.

Quick Sort vs. Other Sorting Algorithms

Quick sort is often compared to other sorting algorithms, such as merge sort, heap sort, and bubble sort, each of which has its own strengths and weaknesses. Understanding these differences can help developers choose the most appropriate sorting algorithm for their specific needs.

Compared to merge sort, quick sort tends to be faster in practice due to its in-place sorting nature, which reduces the need for additional memory allocation. However, merge sort's stability and consistent O(n log n) time complexity make it a better choice for certain applications, particularly when dealing with large datasets or requiring stable sorting.

Heap sort, like quick sort, is an in-place sorting algorithm with an average-case time complexity of O(n log n). However, heap sort's performance can be less predictable, and its implementation is often more complex than that of quick sort.

Bubble sort, on the other hand, is a simple sorting algorithm with a worst-case time complexity of O(n^2). While bubble sort is easy to understand and implement, it is generally not suitable for large datasets due to its inefficiency compared to quick sort and other more advanced algorithms.

By comparing quick sort to these alternatives, developers can better understand its strengths and limitations and make informed decisions about which sorting algorithm to use in their specific applications.

Applications of Quick Sort

Quick sort's efficiency and adaptability make it well-suited for a wide range of applications across various domains. Some common use cases for quick sort include:

• Data analysis: Quick sort is often used to organize large datasets for analysis, allowing researchers and analysts to quickly access and interpret the data.
• Database management: Sorting plays a crucial role in database operations, and quick sort's efficiency makes it a valuable tool for managing and organizing records.
• Computer graphics: In computer graphics, quick sort can be used to sort geometric data, such as vertices and edges, for rendering and display purposes.
• Networking: Quick sort is used in networking applications to sort packets and manage data transmission, ensuring efficient data handling and communication.

These applications demonstrate quick sort's versatility and highlight its continued relevance in various industries and fields.

Implementing Quick Sort in Code

Implementing quick sort in code involves translating the algorithm's logical steps into a programming language. While the specific syntax may vary depending on the language used, the basic structure of the quick sort algorithm remains consistent.

Here is a simple implementation of quick sort in Python:

 def quick_sort(arr): if len(arr) pivot] return quick_sort(left) + middle + quick_sort(right) 

This implementation uses a recursive approach and the median-of-three pivot selection strategy. It demonstrates the key steps of the quick sort algorithm: selecting a pivot, partitioning the array, and recursively sorting the sub-arrays.

By understanding the implementation of quick sort, developers can customize and optimize the algorithm to address specific challenges and requirements in their applications.

Optimizing Quick Sort

Optimizing quick sort involves implementing various strategies to enhance its performance and address potential limitations. Some common optimization techniques include:

• Pivot selection: Choosing an appropriate pivot is crucial for achieving balanced partitions and maintaining quick sort's average-case efficiency. Strategies such as random pivot selection and median-of-three pivot selection can help improve performance.
• Tail recursion: By converting recursive calls into tail-recursive calls, developers can reduce the algorithm's reliance on the call stack and minimize the risk of stack overflow.
• Switching to insertion sort: For small sub-arrays, quick sort's overhead may outweigh its benefits. In such cases, switching to insertion sort for small sub-arrays can improve overall performance.
• Iterative implementation: Implementing quick sort iteratively can further reduce the risk of stack overflow and improve memory usage.

These optimization techniques enable developers to fine-tune quick sort's performance and ensure its suitability for a wide range of applications and datasets.

Common Misconceptions

Despite its widespread use and recognition, quick sort is often subject to misconceptions and misunderstandings. Some common misconceptions include:

• Quick sort is always the fastest sorting algorithm: While quick sort is efficient in many scenarios, its performance can be affected by factors such as pivot selection and input order. It is not universally the fastest sorting algorithm for all datasets.
• Quick sort is unstable: While the basic implementation of quick sort is unstable, meaning it does not preserve the relative order of equal elements, stability can be achieved through modifications and optimizations.
• Quick sort always uses recursion: While recursion is a common approach to implementing quick sort, iterative implementations exist and can offer advantages in terms of performance and memory usage.

By addressing these misconceptions, developers can gain a clearer understanding of quick sort's behavior and capabilities, enabling them to make informed decisions about its use in their applications.

Frequently Asked Questions

Here are some frequently asked questions about quick sort:

1. What is the main advantage of quick sort? The main advantage of quick sort is its efficiency, particularly for large datasets, due to its average-case time complexity of O(n log n).
2. Is quick sort a stable sorting algorithm? Quick sort is not inherently stable, but stability can be achieved through modifications and optimizations.
3. How does quick sort compare to merge sort? Quick sort is generally faster in practice due to its in-place sorting nature, but merge sort offers stability and consistent performance for certain applications.
4. What are the risks of using quick sort? The main risks of using quick sort include encountering its worst-case time complexity and stack overflow issues due to its recursive nature.
5. Can quick sort be parallelized? Yes, quick sort's divide-and-conquer strategy lends itself well to parallelization, allowing for performance improvements on multi-core processors.
6. What are some common optimizations for quick sort? Common optimizations for quick sort include random pivot selection, tail recursion, switching to insertion sort for small sub-arrays, and iterative implementations.

Conclusion

Quick sort is a remarkable sorting algorithm that has stood the test of time, thanks to its efficiency, adaptability, and elegance. By understanding its principles, advantages, and limitations, developers can harness quick sort's power to address a wide range of sorting challenges across various domains.

As we have explored in this comprehensive guide, quick sort's success lies in its divide-and-conquer strategy, which enables it to efficiently organize large datasets with minimal resource usage. With careful pivot selection, optimization techniques, and a clear understanding of its behavior, quick sort can continue to be a valuable tool in the world of computer science and beyond.

For further reading on sorting algorithms and optimization techniques, visit GeeksforGeeks, a reputable resource for computer science concepts and programming practices.