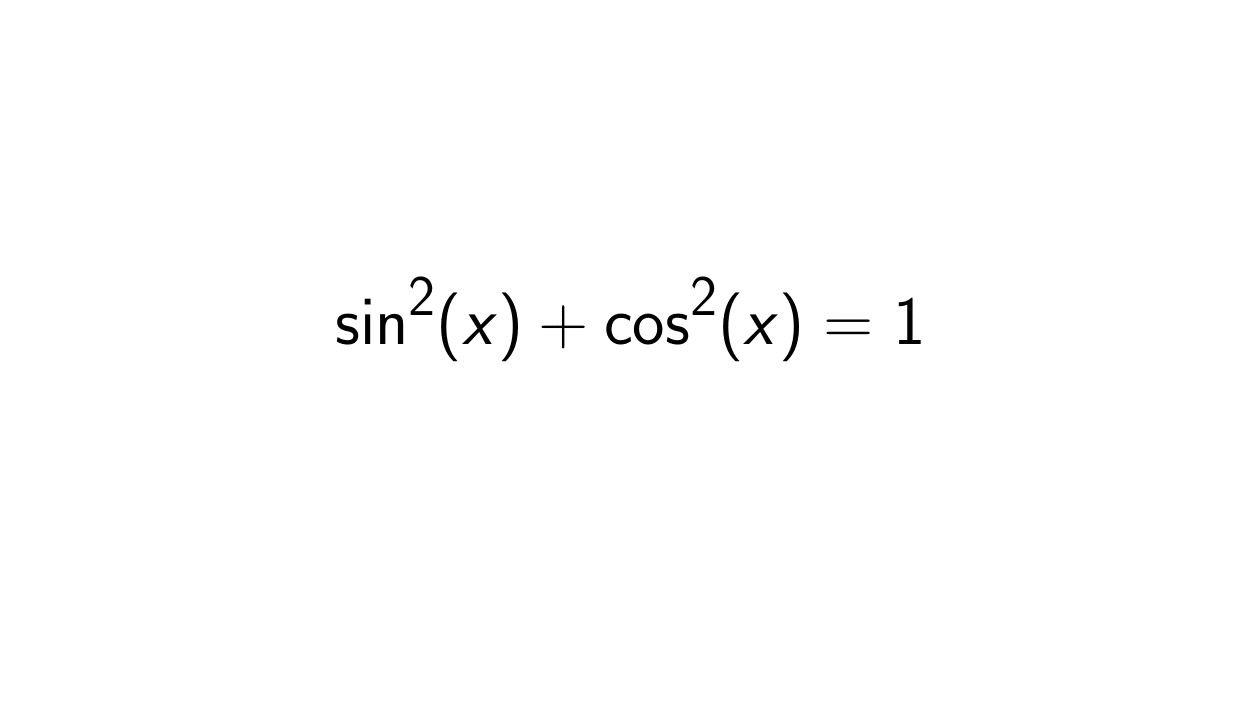Exploring The Intricacies Of Cos 2 Sin 2 1

The realm of trigonometry often presents intriguing combinations that can perplex even the most seasoned mathematicians. One such combination is the expression "cos 2 sin 2 1," which opens the door to a multitude of mathematical explorations. Whether you are a student, a teacher, or simply a math enthusiast, understanding the implications of this expression can significantly enhance your mathematical skills and insights. In this article, we will delve into the intricacies of "cos 2 sin 2 1," exploring its components, applications, and relevance in various mathematical contexts. We will also touch on how it relates to other trigonometric identities and their practical uses in real-world scenarios.

The expression "cos 2 sin 2 1" can be broken down into its fundamental parts: cosine and sine functions, and the angles involved. Recognizing the relationship between these functions is key to unearthing their underlying properties. As we navigate through this topic, we will uncover specific examples and applications that reflect the importance of trigonometric identities in both theoretical and practical mathematics.

Furthermore, we will address common questions surrounding "cos 2 sin 2 1," including how to compute it, its significance in various fields, and how it relates to other mathematical concepts. By the end of this article, readers will have a clearer understanding of this particular expression and its broader implications in the world of mathematics.

Read also:

The Comprehensive Guide To Understanding T65533rban A Look Into Its Cultural Historical And Social Significance

What is the Significance of Cos 2 Sin 2 1?

Understanding the significance of "cos 2 sin 2 1" is crucial for students and professionals alike. This expression combines two fundamental trigonometric functions, cosine and sine, which are essential in various fields such as physics, engineering, and computer science. The importance of knowing how to manipulate and apply these functions cannot be overstated.

How is Cos 2 Sin 2 1 Calculated?

To calculate "cos 2 sin 2 1," one must first break it down into manageable parts. Here’s a simple breakdown of the steps you might take:

1. Identify the angles involved in the expression.
2. Calculate the sine of the angle (in this case, 2 and 1).
3. Calculate the cosine of the angle (in this case, 2).
4. Combine the results according to the expression.

Can Cos 2 Sin 2 1 be Simplified?

Yes, mathematical expressions often can be simplified using various identities. For "cos 2 sin 2 1," we can utilize trigonometric identities such as the double angle formulas. These identities can help transform the expression into a more manageable form, making it easier to work with in calculations.

What Real-World Applications Does Cos 2 Sin 2 1 Have?

The practical applications of "cos 2 sin 2 1" extend beyond the classroom. In fields such as physics, engineering, and computer graphics, understanding trigonometric functions is vital. Here’s how this expression can be relevant:

• Physics: Trigonometric functions help in analyzing wave patterns, oscillations, and other phenomena.
• Engineering: These calculations are essential in designing structures, understanding forces, and analyzing motion.
• Computer Graphics: Trigonometric identities are used to create realistic animations and graphical representations.

Are There Similar Expressions to Cos 2 Sin 2 1?

Many trigonometric expressions share similarities with "cos 2 sin 2 1." For instance, "sin 2 cos 2 1" or "cos 2 + sin 2" can yield different results but are often used in similar contexts. Understanding these variations can provide deeper insights into the behavior of trigonometric functions.

What Are the Common Misunderstandings About Cos 2 Sin 2 1?

Many students encounter misunderstandings when dealing with trigonometric expressions. Some common misconceptions include:

Read also:

The Empowering Journey Of The Chubby Girl Embracing Body Positivity And Confidence

• Believing that cosine and sine functions are interchangeable.
• Not recognizing the impact of angles on the results.
• Failing to apply the correct identities when simplifying.

What Resources Can Help in Understanding Cos 2 Sin 2 1?

For those looking to deepen their understanding of "cos 2 sin 2 1," various resources are available:

• Textbooks: Many mathematics textbooks cover trigonometric functions in detail.
• Online Tutorials: Websites and video platforms offer tutorials that break down these concepts.
• Mathematical Software: Tools like MATLAB or GeoGebra can visualize trigonometric functions and their behaviors.

What Challenges Might One Face When Studying Cos 2 Sin 2 1?

Studying any mathematical concept comes with its challenges. When dealing with "cos 2 sin 2 1," students may struggle with:

• Understanding the foundational concepts of sine and cosine.
• Applying the correct identities and formulas.
• Visualizing the functions and their interactions.

Conclusion: Why Should You Explore Cos 2 Sin 2 1?

Exploring "cos 2 sin 2 1" is an endeavor that can enhance your mathematical prowess and understanding of trigonometric identities. This expression is not just a series of letters and symbols; it represents the foundation of many concepts in mathematics and its applications in the real world. By familiarizing yourself with "cos 2 sin 2 1," you are equipping yourself with valuable skills that will serve you well in various fields and endeavors.