Understanding The Temperature Dependant Band Gap Energy Graph For Conventional Superconductors

The field of superconductivity has long fascinated scientists and researchers, as it holds the key to revolutionary advancements in energy transmission, magnetic levitation, and quantum computing. Among the various properties studied in superconducting materials, the temperature dependent band gap energy graph serves as a critical tool in understanding the behavior of these materials at different temperatures. This graph illustrates how the band gap energy of conventional superconductors evolves with temperature, shedding light on the underlying mechanisms that govern superconductivity.

As temperature changes, the electronic properties of conventional superconductors also transform, which can significantly influence their performance and applications. The interplay between temperature and band gap energy is essential for optimizing the design and functionality of superconducting materials. Grasping the nuances of the temperature dependant band gap energy graph is therefore vital for both theoretical exploration and practical implementation in technology.

In this article, we will delve into the intricacies of the temperature dependant band gap energy graph for conventional superconductors. By addressing key questions and exploring relevant concepts, we aim to provide a comprehensive overview that benefits both seasoned researchers and newcomers to the field of superconductivity.

Read also:

The Comprehensive Guide To Sounding Rods Understanding Safety And Techniques

What is the Band Gap Energy in Conventional Superconductors?

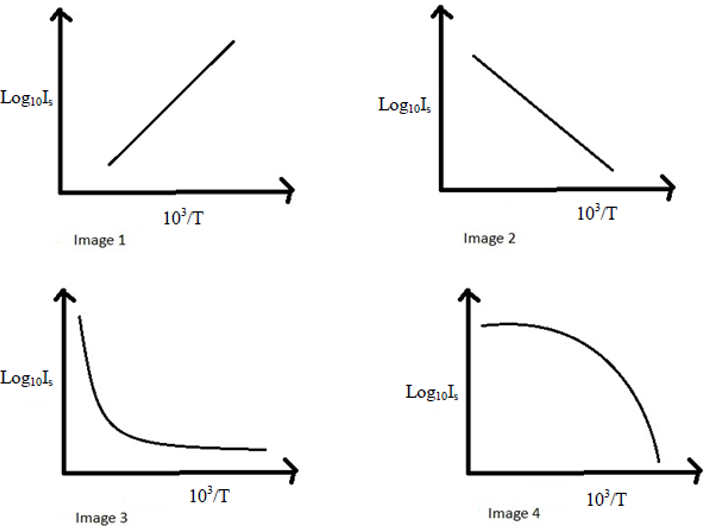
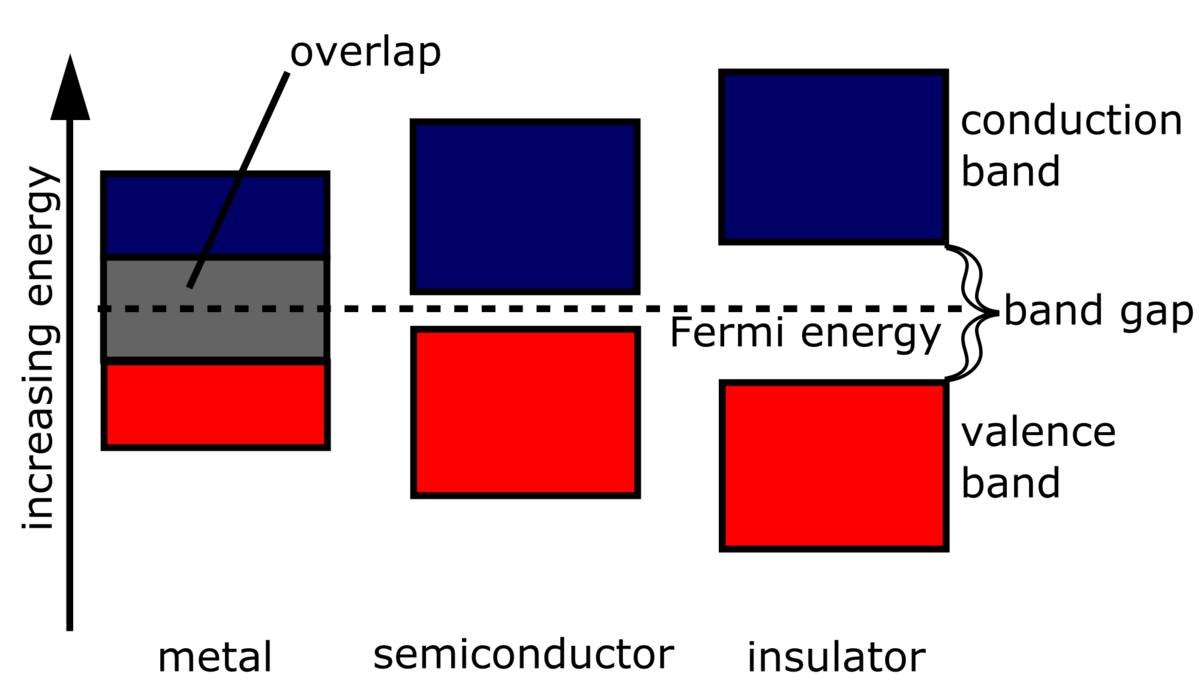
The band gap energy is a fundamental property of materials that describes the energy difference between the top of the valence band and the bottom of the conduction band. In conventional superconductors, this energy plays a crucial role in determining the material's electronic and thermal properties. When the temperature is lowered, the band gap energy typically decreases, facilitating the pairing of electrons into Cooper pairs, which are essential for the superconducting state.

How Does Temperature Affect Band Gap Energy?

Temperature has a profound impact on the band gap energy of superconductors. As the temperature increases, thermal vibrations can disrupt the electron pairing process, leading to a reduction in superconductivity. The temperature dependant band gap energy graph illustrates this relationship, showcasing the nonlinear behavior of band gap energy as the temperature varies.

What Does the Temperature Dependant Band Gap Energy Graph Look Like?

The temperature dependant band gap energy graph typically features a downward curve, indicating that as temperature rises, the band gap energy decreases. This graph is crucial for understanding the critical temperature (Tc) at which a material transitions from a normal state to a superconducting state. The graph provides insights into the range of temperatures over which superconductivity can be sustained and helps identify materials with desirable superconducting properties.

Why is the Temperature Dependant Band Gap Energy Graph Important?

The temperature dependant band gap energy graph is essential for several reasons:

• It helps identify the critical temperature for superconductivity.
• It informs the selection of materials for specific applications.
• It aids in understanding the mechanisms behind superconductivity.
• It provides a framework for exploring new superconducting materials.

How Can We Measure Band Gap Energy in Superconductors?

Measuring the band gap energy in superconductors involves various techniques, including:

1. Optical spectroscopy: This method utilizes light to probe the electronic transitions in the material, providing insights into the band structure.
2. Angle-resolved photoemission spectroscopy (ARPES): ARPES is an advanced technique that allows for the mapping of the electronic band structure of materials.
3. Scanning tunneling microscopy (STM): STM can be used to investigate the local electronic properties of superconductors on a nanometer scale.

What Role Do Phonons Play in the Band Gap Energy of Superconductors?

Phonons, which are quantized modes of vibrations in a lattice structure, play a significant role in the behavior of superconductors. They facilitate the interaction between electrons, leading to the formation of Cooper pairs. As the temperature changes, the phonon spectrum also alters, which can directly affect the band gap energy. Understanding these interactions is crucial for developing better superconducting materials.

Read also:

The Dynamic Journey Of Nct 127 Members Exploring Their Lives And Impact

What are the Future Directions in Superconductivity Research?

The future of superconductivity research is bright, with several avenues to explore:

• Investigating high-temperature superconductors to understand their unique properties.
• Developing novel materials that exhibit superconductivity at room temperature.
• Utilizing advanced computational methods to predict band gap energy behavior.
• Exploring the interplay between superconductivity and other electronic phases.

Conclusion: The Significance of the Temperature Dependant Band Gap Energy Graph for Conventional Superconductors

In summary, the temperature dependant band gap energy graph for conventional superconductors is a fundamental tool in the study of superconductivity. By illustrating how band gap energy changes with temperature, this graph provides insights into the mechanisms of superconductivity, informs material selection, and guides future research. As scientists continue to explore this fascinating field, the knowledge gained from these graphs will undoubtedly lead to advancements in technology and a deeper understanding of the underlying physics of superconductors.