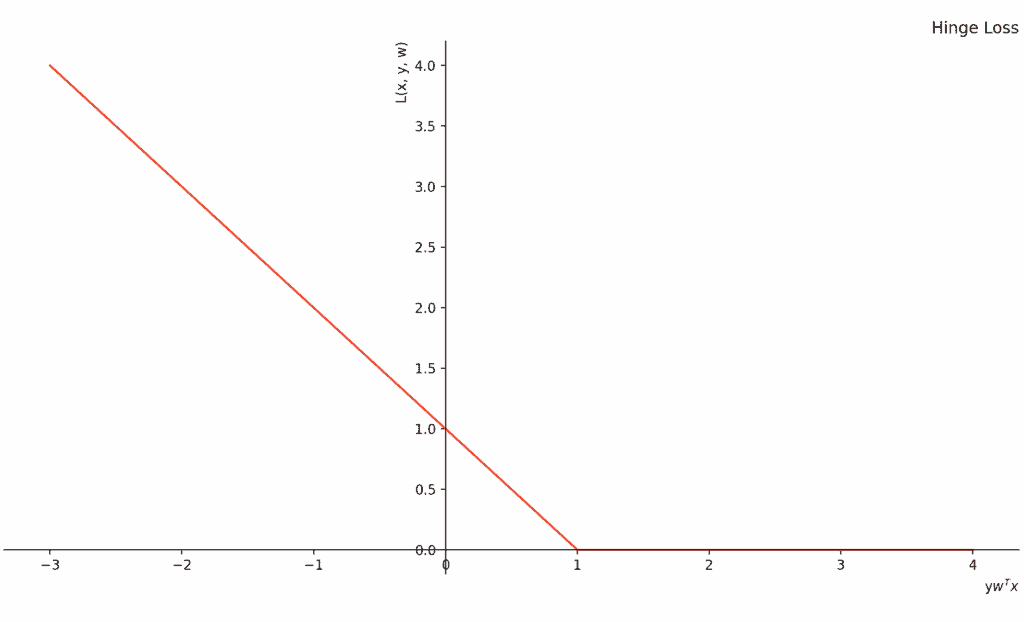Understanding The Subgradient For Hinge Loss In Machine Learning

In the world of machine learning, loss functions play a pivotal role in determining how well a model performs. One such function that has gained significant attention is the hinge loss, particularly in support vector machines (SVMs). The subgradient for hinge loss is a crucial concept that helps in optimizing the learning process by providing a way to handle non-differentiable points in the loss function. By understanding the intricacies of the subgradient, researchers and practitioners can effectively train models that achieve better classification results.

The hinge loss function is primarily used for "maximum-margin" classification, especially in scenarios involving binary classification. It calculates the error between the predicted output and the actual class label. However, the challenge arises when the hinge loss is not differentiable at certain points, which makes traditional optimization techniques less effective. This is where the concept of the subgradient comes into play, offering a way to navigate these non-differentiable regions and still make progress in the optimization process.

In this article, we will explore the subgradient for hinge loss in depth, discussing its mathematical formulation, properties, and practical implications in machine learning. We will also address common questions surrounding its application, ensuring that you have a comprehensive understanding of this essential concept. Whether you are a seasoned data scientist or a newcomer to the field, mastering the subgradient for hinge loss will undoubtedly enhance your ability to develop robust machine learning models.

Read also:

The Comprehensive Guide Is Weed Legal In Texas

What is the Hinge Loss Function?

The hinge loss function is defined as follows:

Hinge Loss = max(0, 1 - y * f(x))

Where:

• y is the true class label (either +1 or -1)
• f(x) is the prediction made by the model

The hinge loss is zero when the prediction is correct and sufficiently far away from the decision boundary. However, it increases linearly when the prediction is incorrect or too close to the boundary.

How is the Subgradient Defined for Hinge Loss?

The subgradient of a function at a given point provides a generalization of the gradient, allowing for optimization techniques even in non-differentiable scenarios. For the hinge loss, the subgradient can be expressed as:

subgradient = {0, if y * f(x) > 1; -y * x, if y * f(x) < 1; undefined, if y * f(x) = 1}

Read also:

Explore Mesa Verde National Park Colorados Ancient Heritage

This formulation highlights that when the prediction is correct and sufficiently distant from the margin (i.e., y * f(x) > 1), the subgradient is zero, indicating no need for adjustment. Conversely, when the prediction is incorrect or too close to the margin, the subgradient guides the adjustment in the direction of the true label.

What are the Properties of the Subgradient for Hinge Loss?

The subgradient for hinge loss possesses several important properties:

• Non-differentiability: The hinge loss is non-differentiable at the points where the prediction exactly meets the margin.
• Piecewise Linear: The hinge loss function is piecewise linear, meaning that it can be broken down into linear segments, which is beneficial for optimization.
• Robustness: The subgradient provides a robust way to handle cases where traditional gradients fail, particularly in SVMs.

How Can the Subgradient for Hinge Loss be Used in Machine Learning?

When training models, the subgradient for hinge loss can be utilized in various optimization algorithms, including:

• Subgradient Descent: This method involves using the subgradient to iteratively update model parameters.
• Stochastic Subgradient Descent: A variation that utilizes mini-batches of data to compute subgradients, enhancing convergence speed.
• Proximal Methods: These methods leverage the subgradient for hinge loss while incorporating regularization to prevent overfitting.

What Challenges are Associated with the Subgradient for Hinge Loss?

While the subgradient for hinge loss is a powerful tool, it comes with its own set of challenges:

• Convergence Speed: The convergence speed of subgradient descent can be slower compared to gradient descent due to the non-smooth nature of the hinge loss.
• Tuning Hyperparameters: The performance of algorithms using subgradients may depend heavily on the choice of hyperparameters, such as learning rates.
• Handling Non-differentiable Points: Properly managing the undefined points of the subgradient can be complex and may require additional strategies.

How to Implement the Subgradient for Hinge Loss in Code?

Implementing the subgradient for hinge loss in programming languages like Python can be accomplished using libraries such as NumPy. Here is a basic example:

 def subgradient_hinge_loss(y, f, x): if y * f > 1: return 0 elif y * f < 1: return -y * x else: return None # Undefined point 

This function takes the true label y, the prediction f, and the input features x, returning the appropriate subgradient value based on the hinge loss definition.

What are the Future Directions in Research on Subgradient for Hinge Loss?

As machine learning continues to evolve, research on the subgradient for hinge loss is likely to explore several avenues:

• Hybrid Models: Combining hinge loss with other loss functions and exploring their subgradients to improve model performance.
• Adaptive Learning Rates: Developing methods to adaptively tune learning rates when using subgradient descent for hinge loss.
• Robust Optimization: Investigating ways to enhance the robustness of subgradient methods in the face of noisy data.