Understanding The Concept Of Ln A X: A Deep Dive

In the realm of mathematics, particularly in calculus and algebra, the natural logarithm, denoted as ln, plays a crucial role in various applications. The expression "ln a x" combines the natural logarithm with variables that can represent different values, making it a fundamental concept in mathematical analysis. This article aims to demystify ln a x, providing insights into its significance, applications, and the underlying principles that govern its behavior.

The natural logarithm is the logarithm to the base e, where e is an irrational constant approximately equal to 2.71828. Understanding ln a x is essential for students and professionals alike, as it frequently appears in calculus, particularly in differentiation and integration. By exploring the properties of natural logarithms, we can better comprehend their impact on various mathematical functions and real-world scenarios.

This article will explore the significance of ln a x through various headings and subheadings, addressing key questions and concepts that will enrich your understanding of this important mathematical function. Whether you're a student seeking clarification or a professional looking to refresh your knowledge, this guide will provide comprehensive insights into the world of ln a x.

Read also:

Exploring The World Of Cute Cars A Delightful Journey Into Adorable Automobile Designs

What is ln a x and How is it Used?

ln a x represents the natural logarithm of the product of a and x, revealing the relationship between multiplication and logarithmic functions. The expression can be broken down as follows:

ln a x = ln a + ln x

This property illustrates how the natural logarithm of a product can be expressed as the sum of the natural logarithms of its factors. This fundamental principle is utilized in various mathematical calculations and proofs.

How Do You Calculate ln a x?

Calculating ln a x involves understanding the values of a and x. Here’s a step-by-step guide:

1. Determine the values of a and x.
2. Calculate ln a and ln x separately.
3. Add the two results together to obtain ln a x.

For example, if a = 2 and x = 3, then:

ln 2 + ln 3 = ln (2 * 3) = ln 6

Read also:

The Fascinating Czech Wolf Dog A Comprehensive Guide

What are the Applications of ln a x?

The applications of ln a x are extensive and diverse, spanning various fields such as:

• Finance: Used in calculating compound interest and growth rates.
• Physics: Appears in equations related to decay and growth processes.
• Statistics: Essential for understanding logarithmic transformations in data analysis.
• Engineering: Applied in thermodynamics and systems dynamics.

What are the Properties of ln a x?

Understanding the properties of ln a x can help in simplifying complex equations. Some key properties include:

• ln 1 = 0: The natural logarithm of one is always zero.
• ln e = 1: The natural logarithm of the base e equals one.
• ln (a^b) = b * ln a: The logarithm of a power can be expressed as the exponent multiplied by the logarithm of the base.

How Does ln a x Relate to Exponential Functions?

The relationship between ln and exponential functions is foundational in calculus. The function e^x is the inverse of ln x, meaning that:

ln(e^x) = x and e^(ln x) = x

This relationship shows how ln a x can be viewed through the lens of exponential growth and decay, providing insights into various mathematical phenomena.

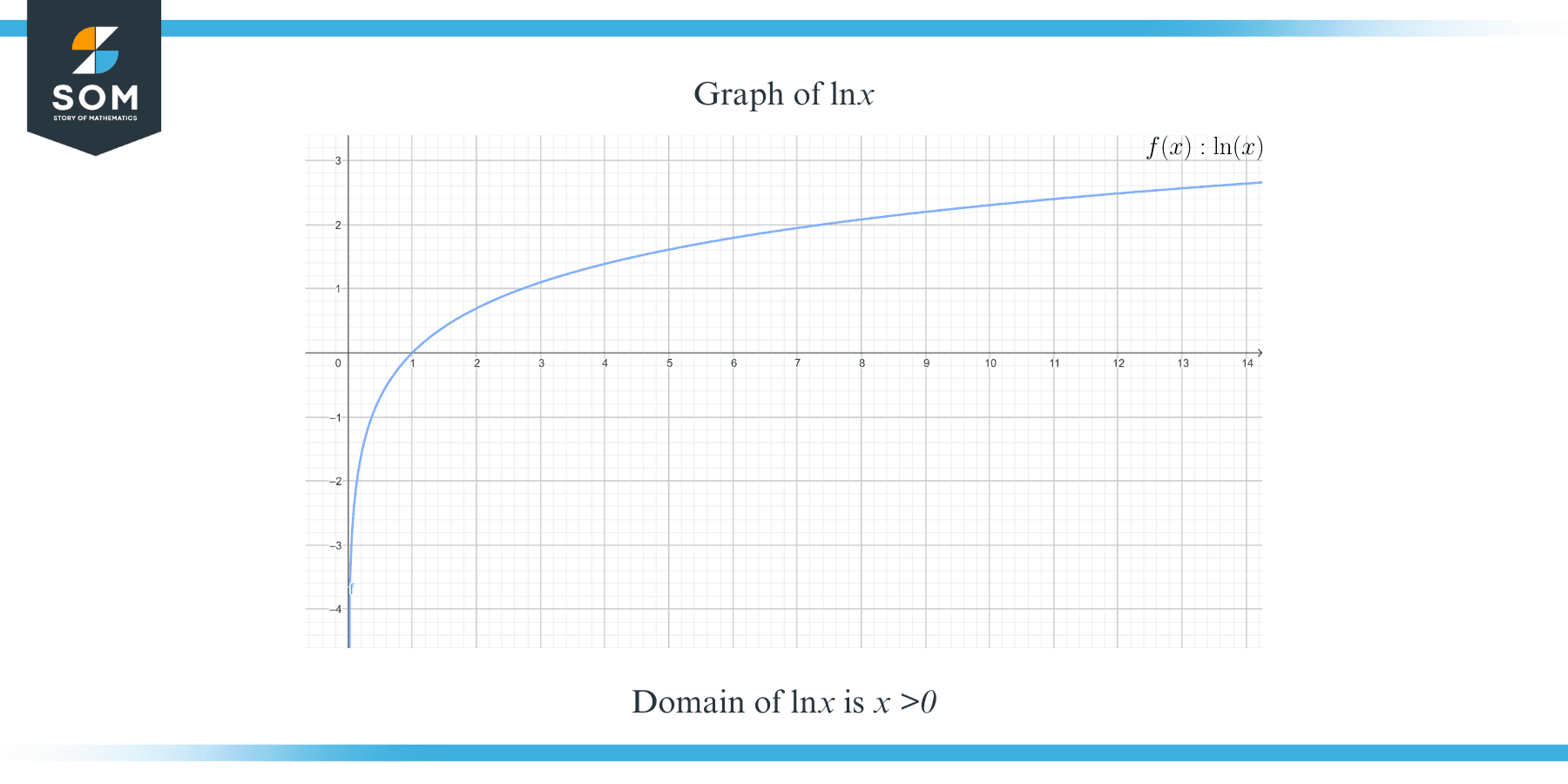
Can You Graph ln a x?

Graphing ln a x can provide a visual understanding of its behavior. The graph of ln x typically increases slowly and approaches negative infinity as x approaches zero. Here’s how you can create a graph:

1. Choose a range of values for x (e.g., 0.1 to 10).
2. Calculate the corresponding values of ln x.
3. Plot the points on a Cartesian plane.

The resulting curve will demonstrate the logarithmic growth of ln x, highlighting its unique properties compared to linear or polynomial functions.

Conclusion: Mastering ln a x

In conclusion, understanding ln a x is vital for anyone delving into mathematics, finance, engineering, or the sciences. The natural logarithm serves as a powerful tool for simplifying and analyzing complex relationships between variables. By grasping the principles and applications of ln a x, you lay a solid foundation for further exploration in mathematics and its various applications. Whether you are working on a mathematical proof, analyzing data, or solving real-world problems, the concept of ln a x will undoubtedly prove invaluable.