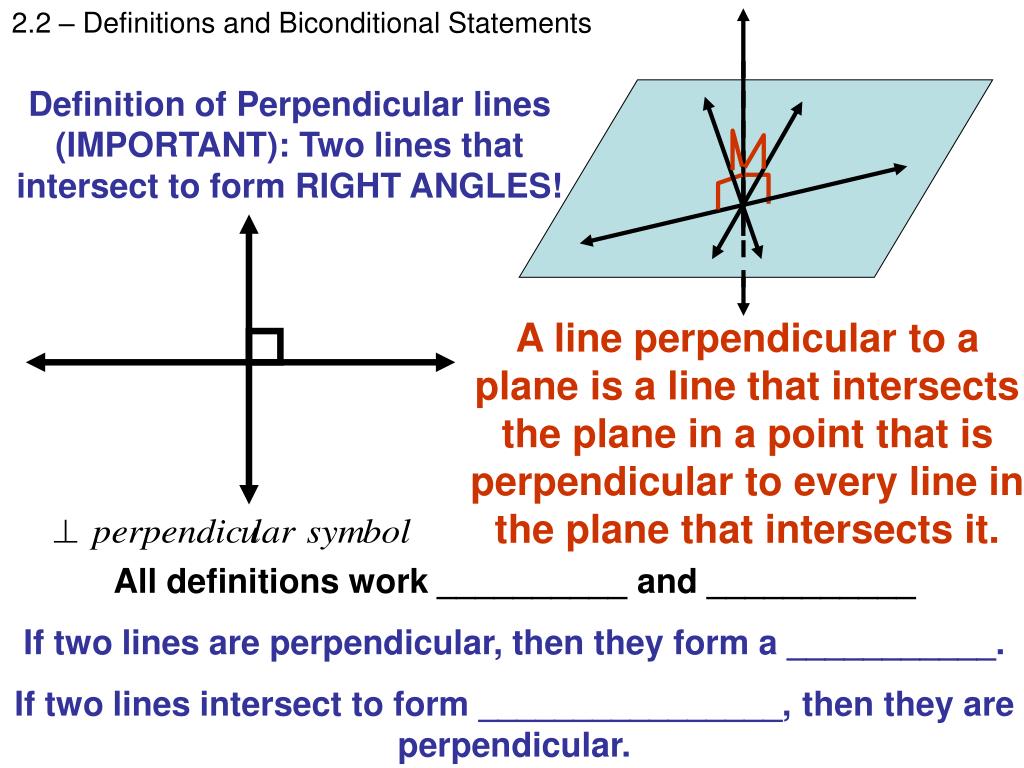
A Line Perpendicular To A Plane: Understanding The Geometry Behind It

In the realm of geometry, the concept of a line perpendicular to a plane is fundamental. It forms the basis of many geometric principles and applications in various fields, including mathematics, engineering, and computer graphics. Understanding this concept not only enhances our comprehension of spatial relationships but also equips us with the tools to tackle complex problems involving three-dimensional structures. What does it mean for a line to be perpendicular to a plane? How do we visualize and apply this concept in real-world scenarios? This article aims to explore these questions and provide a comprehensive understanding of the relationship between lines and planes.

The idea of a line being perpendicular to a plane is essential in various disciplines. For instance, in architecture and engineering, ensuring that certain elements are perpendicular to a plane can be crucial for structural integrity. Furthermore, in the realm of computer graphics, understanding how objects interact with planes helps in rendering realistic images. By delving into the mathematical definitions and visual representations, we can demystify this important geometric concept and grasp its implications in practical applications.

As we embark on this exploration, we will discuss the definition, properties, and applications of a line perpendicular to a plane. We will also address common questions that arise when dealing with this concept, from basic definitions to advanced applications in fields such as mathematics and physics. By the end of this article, readers will have a clear understanding of what it means for a line to be perpendicular to a plane, and how this knowledge can be applied in various contexts.

Read also:

Avril Lavigne 2024 Tour Get Your Tickets Today

What Does It Mean for a Line to be Perpendicular to a Plane?

In geometry, a line is considered perpendicular to a plane if it meets the plane at a right angle, which is 90 degrees. This relationship can be visualized in three-dimensional space, where the line extends out from a point on the plane, forming a right angle with the plane's surface. To better understand this concept, consider the following key points:

• A line perpendicular to a plane intersects the plane at exactly one point.
• The angle formed between the line and any line lying within the plane at the point of intersection is a right angle.
• The perpendicular line can be considered as the shortest distance from the point on the plane to the line extending away from that point.

How Can We Visualize a Line Perpendicular to a Plane?

Visualizing a line perpendicular to a plane can be challenging, especially for those new to geometric concepts. One effective way to imagine this relationship is to think of a pencil standing upright on a flat surface, such as a table. The pencil represents the line, while the table is the plane. The point where the pencil touches the table is the intersection point, and the angle formed between the table and the pencil is a right angle. This simple analogy helps in understanding how a line can be perpendicular to a plane.

What are the Properties of a Line Perpendicular to a Plane?

There are several important properties associated with a line that is perpendicular to a plane:

• The perpendicular line is unique; there can only be one line that is perpendicular to a given plane from a specific point.
• Any line parallel to the perpendicular line will also be perpendicular to the same plane.
• If two lines are both perpendicular to the same plane, they can be parallel to each other or intersect outside the plane.

What are the Applications of a Line Perpendicular to a Plane?

The understanding of lines and planes, particularly the concept of a line perpendicular to a plane, has numerous applications in various fields:

1. In Engineering and Architecture

In engineering and architecture, ensuring that structural elements are perpendicular to certain planes is crucial for maintaining stability and safety. For example, columns must be perpendicular to the floor to ensure that loads are evenly distributed.

2. In Computer Graphics

In computer graphics, the concept of lines being perpendicular to planes is essential for rendering three-dimensional images. This understanding aids in calculating the angles and positions of objects relative to a viewer's perspective.

Read also:

Silly Questions To Ask A Fun Exploration Of The Whimsical Side Of Inquiry

3. In Robotics

Robotics applications also utilize the concept of perpendicular lines and planes. For instance, when programming a robotic arm to pick up an object, ensuring that the arm approaches the object from a direction that is perpendicular to the surface it rests on can improve efficiency and accuracy.

Why is Understanding a Line Perpendicular to a Plane Important?

Grasping the concept of a line perpendicular to a plane is vital for students and professionals in fields such as mathematics, physics, and engineering. It lays the groundwork for more advanced topics, including vector calculus and spatial reasoning, which are essential for solving complex problems in three-dimensional space.

How Can We Calculate a Line Perpendicular to a Plane?

To determine a line that is perpendicular to a given plane, we can use the normal vector of the plane. The normal vector is a vector that is perpendicular to the plane's surface. The steps to find a line perpendicular to a plane are as follows:

1. Identify the equation of the plane, which is typically in the form Ax + By + Cz + D = 0.
2. Extract the coefficients A, B, and C from the plane's equation; these will be the components of the normal vector (N) to the plane.
3. Choose a point (P) on the plane to serve as the line's intersection point.
4. Formulate the equation of the line using the normal vector and the point, represented as P + tN, where t is a scalar parameter.

What Challenges Might Arise When Working with Lines and Planes?

When working with lines and planes, several challenges may arise, including:

• Identifying the correct intersection point between the line and the plane.
• Visualizing the spatial relationships in three-dimensional space.
• Calculating angles and distances accurately.

Conclusion: The Significance of Lines Perpendicular to Planes

In summary, understanding a line perpendicular to a plane is crucial for various applications across multiple disciplines. From engineering and architecture to computer graphics and robotics, this geometric concept plays a significant role in ensuring accuracy, stability, and efficiency. By exploring its definitions, properties, and applications, we can appreciate the importance of this concept in both theoretical and practical contexts.

As we continue to explore the world of geometry, we are reminded of the beauty and complexity of spatial relationships, where lines and planes interact in fascinating ways. Whether we are designing structures, programming robots, or creating visual art, the principles of geometry guide us in our endeavors, making the study of lines perpendicular to planes not only relevant but essential.