Exploring The Mysteries Of The Square Root Of Negative 3

The concept of the square root of negative 3 opens up a fascinating world of mathematics, one that challenges our traditional understanding of numbers and their properties. When we think about square roots, we typically associate them with non-negative values. However, introducing negative numbers into the equation leads us to the realm of complex numbers, a domain filled with intriguing possibilities and applications. The square root of negative 3, denoted as √(-3), is a prime example of how mathematics can stretch our understanding beyond the conventional limits.

In essence, the square root of negative 3 can be expressed in terms of imaginary numbers. This is a significant concept in mathematics, as it allows us to solve equations that would otherwise have no real solutions. By utilizing the imaginary unit "i," where i is defined as the square root of -1, we can rewrite √(-3) as √3 * i. This transformation not only simplifies our calculations but also opens the door to a deeper comprehension of complex numbers and their applications in various fields such as engineering, physics, and computer science.

As we delve deeper into the square root of negative 3, we uncover its relevance in various mathematical theories and real-world applications. From electrical engineering to quantum mechanics, understanding complex numbers and their properties is crucial. This article will explore the foundations of imaginary numbers, the significance of the square root of negative 3, and how these concepts are applied in practical scenarios. Join us on this mathematical journey as we unravel the mysteries behind the square root of negative 3.

Read also:

Discover The Enchanting Alabama Gulf Coast Zoo Your Adventure Awaits

What is the Square Root of Negative 3?

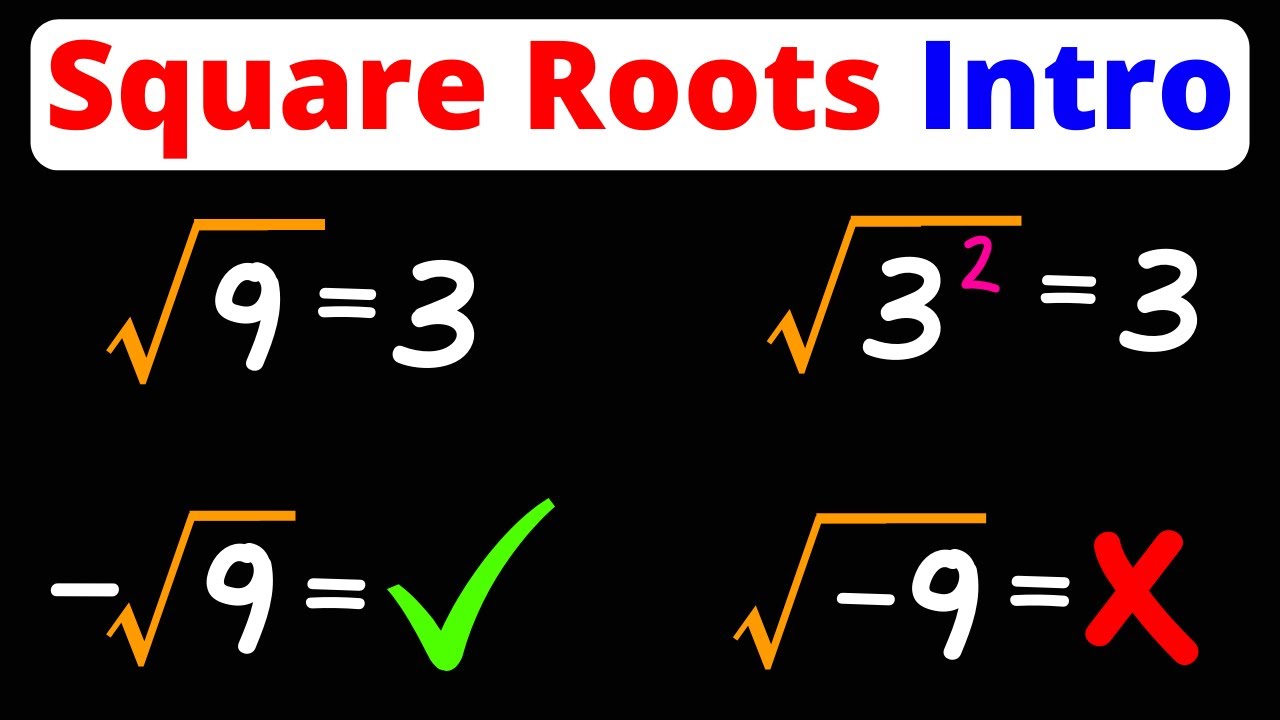
The square root of negative 3 is a mathematical expression that arises when we attempt to find the square root of a negative number. To understand this concept, we need to delve into the realm of complex numbers. The square root of negative 3 can be represented as:

• √(-3) = √3 * i

Here, "i" is the imaginary unit, defined as the square root of -1. Therefore, the square root of negative 3 can be expressed as an imaginary number, which is crucial for solving certain equations in mathematics.

How Do We Calculate the Square Root of Negative 3?

Calculating the square root of negative 3 involves recognizing that we are dealing with an imaginary number. The steps to calculate it are as follows:

1. Identify the negative number: -3.
2. Factor out the negative sign: -3 = -1 * 3.
3. Apply the square root property: √(-3) = √(-1) * √3.
4. Substitute the value of the imaginary unit: √(-1) = i.
5. Combine the results: √(-3) = i√3.

Thus, the square root of negative 3 can be succinctly expressed as i√3.

What Are the Applications of the Square Root of Negative 3?

The square root of negative 3 and complex numbers, in general, have several practical applications across various fields. Some notable areas include:

• Electrical Engineering: Complex numbers are used to analyze AC circuits, where the square root of negative values comes into play.
• Quantum Mechanics: The mathematics of quantum physics often involves complex numbers, including calculations with imaginary units.
• Signal Processing: Complex numbers are fundamental in digital signal processing, where they help in representing waveforms.
• Control Theory: Engineers use complex numbers in system stability analysis and feedback control systems.

Why is the Square Root of Negative 3 Important in Mathematics?

The square root of negative 3 is significant in mathematics for several reasons:

Read also:

Discover The Real Name Of The Radiant Star Jojo Siwa

1. It illustrates the concept of imaginary numbers, which extend the real number system.
2. It aids in solving polynomial equations that do not have real solutions.
3. It contributes to the development of various mathematical theories, such as calculus and linear algebra.

Can We Visualize the Square Root of Negative 3?

Yes, we can visualize the square root of negative 3 in the complex plane. The complex plane is a two-dimensional space where the x-axis represents the real part of a complex number, and the y-axis represents the imaginary part. In this context, the square root of negative 3 can be represented as a point located at (0, √3) on the imaginary axis.

What is the Relationship Between the Square Root of Negative 3 and Other Imaginary Numbers?

The square root of negative 3 has relationships with other imaginary numbers through various mathematical operations. For instance, when multiplied by other imaginary units, it can contribute to forming complex numbers with diverse properties. Additionally, it is associated with the unit circle in trigonometry, where it helps define trigonometric functions in the context of imaginary numbers.

Who Uses the Square Root of Negative 3 in Their Work?

Professionals in various fields utilize the square root of negative 3 in their work, including:

• Mathematicians: They study complex numbers and their properties.
• Engineers: They apply complex numbers in electrical and mechanical systems.
• Physicists: They use complex numbers to model quantum states.
• Computer Scientists: They implement algorithms that may require complex calculations.

How Does Understanding the Square Root of Negative 3 Benefit Students?

For students, grasping the concept of the square root of negative 3 is essential for several reasons:

• It enhances problem-solving skills by encouraging creative thinking.
• It lays the foundation for more advanced mathematical concepts.
• It prepares students for real-world applications in science and engineering.

Conclusion: The Square Root of Negative 3 as a Gateway to Complex Numbers

The square root of negative 3 is more than just a mathematical curiosity; it serves as a gateway to understanding complex numbers and their applications. By embracing the concept of imaginary numbers, we unlock a plethora of possibilities in various scientific and engineering fields. As we continue to explore the intricacies of mathematics, the square root of negative 3 will undoubtedly remain a significant player in our journey of discovery.