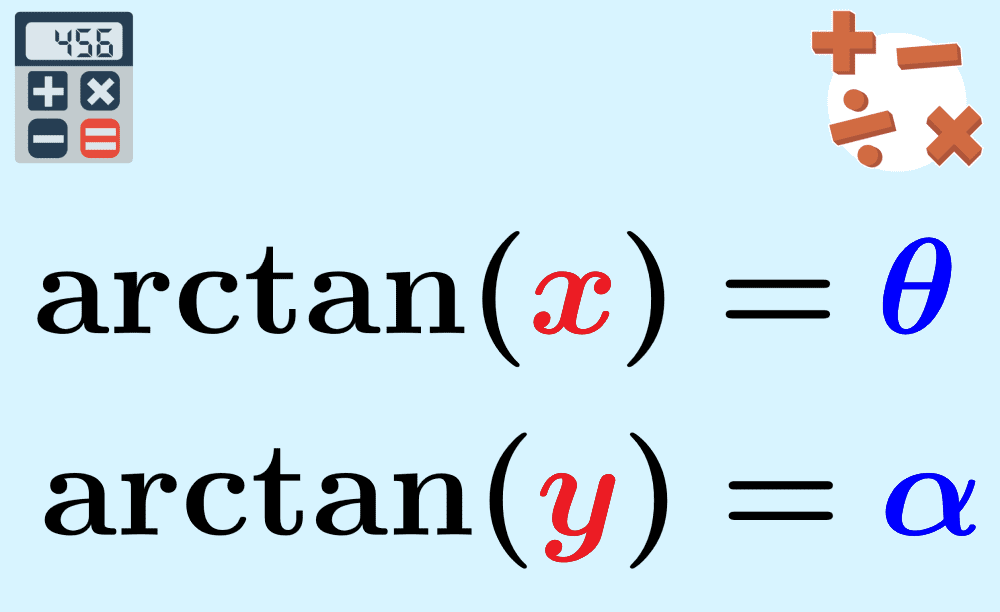Exploring The Depths Of Mathematica Arctan: A Comprehensive Guide

Understanding the concept of arctangent is essential for anyone venturing into the realm of mathematics and computational software. Mathematica, a powerful computational tool developed by Wolfram Research, offers robust functionalities that include the calculation and visualization of arctangent functions. Whether you are a student, educator, or a professional mathematician, mastering the use of Mathematica for arctan will enhance your analytical capabilities and streamline your problem-solving process.

The arctan function, or inverse tangent, is a fundamental mathematical function that allows for the determination of angles from their tangent values. In Mathematica, this function is not only accessible but also provides various options for manipulation and visualization. By diving into the intricacies of Mathematica's arctan, users can explore its applications, from simple calculations to complex graphical representations.

In this article, we will delve deeper into the Mathematica arctan function, answering critical questions and providing examples to enhance your understanding. Whether you are looking to reinforce your mathematical foundation or apply these concepts in real-world scenarios, this guide will serve as a valuable resource.

Read also:

Finding The Best Tire Services Mavis Tire Near Me

What is the Arctan Function in Mathematics?

The arctan function, denoted as arctan(x) or tan^-1(x), is the inverse of the tangent function. It takes a real number x and returns the angle θ whose tangent is x. This relationship is crucial in various fields of study, including trigonometry, physics, and engineering. The arctan function is defined for all real numbers, and its output is typically constrained between -π/2 and π/2 radians, or -90° and 90° degrees.

How Does Mathematica Handle Arctan Calculations?

Mathematica simplifies the computation of the arctan function through its built-in functions. To calculate the arctangent of a number, you can use the command:

ArcTan[x]

This command returns the angle in radians. Mathematica also allows for the calculation of the arctan of complex numbers, providing results that include both real and imaginary components.

What Are the Applications of Mathematica Arctan?

The applications of the arctan function in Mathematica are vast and varied. Some of the key applications include:

• Solving trigonometric equations.
• Modeling periodic phenomena in physics.
• Graphing functions for visual analysis.
• Computing angles in engineering designs.

How Can You Visualize Arctan in Mathematica?

Visualization is a powerful feature of Mathematica that allows users to comprehend mathematical concepts intuitively. To visualize the arctan function, you can use the following command:

Plot[ArcTan[x], {x, -10, 10}]

This command generates a graph of the arctan function over the specified range, providing a clear view of its behavior as x approaches positive and negative infinity.

Read also:

Amy Robach And Tj Holmes Relationship Timeline And Fallout

Can Mathematica Handle Multiple Arguments for Arctan?

Yes, Mathematica can compute the arctan of multiple arguments. The function ArcTan can take two arguments, which represent the coordinates of a point on the Cartesian plane. The command is structured as follows:

ArcTan[x, y]

This function computes the angle formed by the point (x, y) with respect to the origin, offering a geometric interpretation of the arctan function.

What Are Some Common Errors When Using Mathematica Arctan?

While working with the arctan function in Mathematica, users may encounter several common errors, including:

• Incorrect input format (e.g., providing a string instead of a number).
• Assuming that the output is always in degrees (it is in radians by default).
• Forgetting to consider the periodic nature of the tangent function when interpreting results.

How to Troubleshoot Mathematica Arctan Issues?

When facing issues with the arctan function in Mathematica, consider the following troubleshooting steps:

1. Double-check the input values for correctness.
2. Use the function FullForm to understand the structure of your input.
3. Consult the Mathematica documentation for examples and syntax guidelines.

Conclusion: Mastering Mathematica Arctan for Enhanced Mathematical Proficiency

In conclusion, understanding the Mathematica arctan function is essential for those looking to deepen their mathematical knowledge and application skills. By mastering its calculations and visualizations, users can unlock new dimensions of analysis and problem-solving. Whether you are a beginner or an advanced user, the insights provided in this guide will enhance your experience with Mathematica and empower you to tackle complex mathematical challenges with confidence.