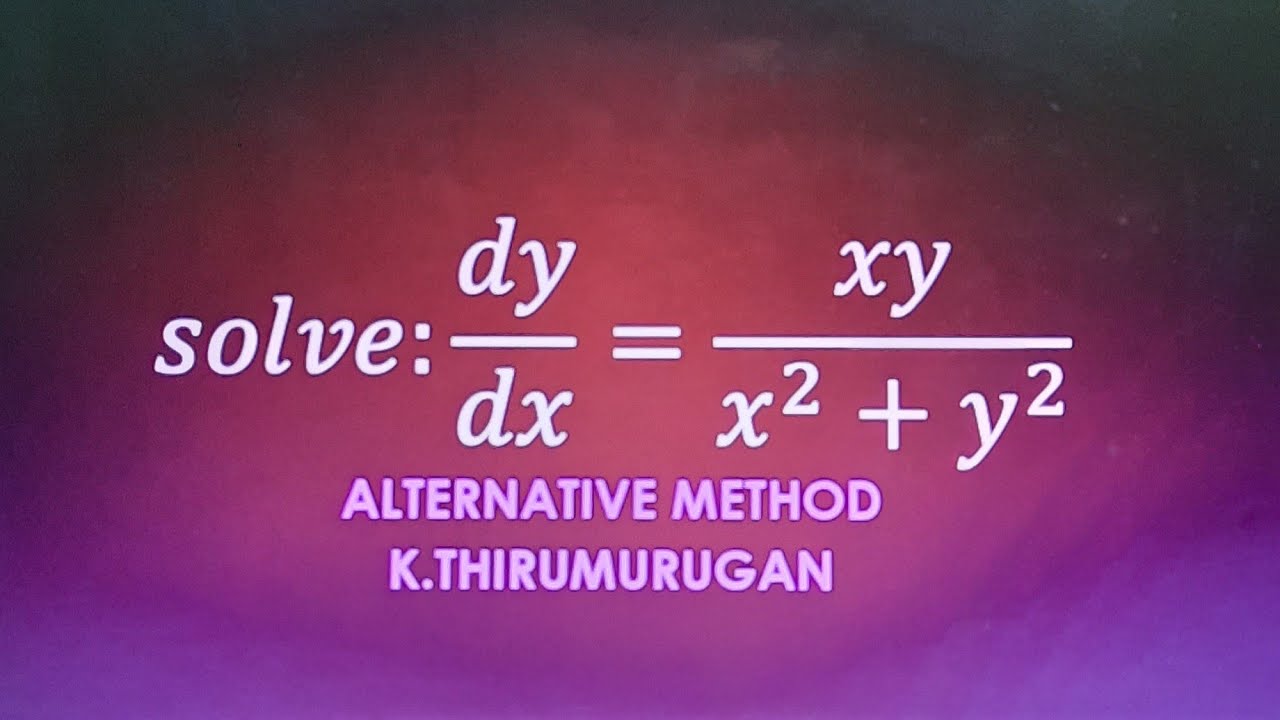Understanding Dy Dx Xy 2: A Comprehensive Guide

In the realm of mathematics, particularly in calculus, the notation "dy dx" often represents the derivative of a function. The expression "xy 2" can introduce complexity in various mathematical operations, making it a worthy subject of exploration. Understanding the relationship between these terms can enhance our grasp of differential equations and their applications across numerous fields.

As we delve deeper into the concept of "dy dx xy 2," we will uncover how these mathematical notations relate to one another, and how they can be used to solve complex equations. This article aims to provide insights into the intricate world of derivatives, with a particular focus on the implications of "dy dx xy 2" in practical scenarios.

Moreover, we will answer crucial questions that arise in the study of calculus, helping both beginners and seasoned mathematicians enhance their understanding. By the end of this article, readers will not only be informed about "dy dx xy 2," but also equipped with the knowledge to apply this understanding effectively.

Read also:

Frontier Airlines Safety Record And Reviews Unraveled

What is the significance of dy dx in calculus?

The notation "dy dx" refers to the derivative of a function in relation to its variable. In calculus, this is foundational for understanding how functions change. Essentially, the derivative measures the rate at which one quantity changes in relation to another, providing insights into the behavior of functions.

How does dy dx relate to the concept of slopes?

The derivative can be interpreted as the slope of the tangent line to a curve at a given point. This relationship is crucial in various applications, including physics, engineering, and economics, where understanding rates of change is essential. By calculating "dy dx," one can derive important information about the function's behavior, such as identifying maximum and minimum values.

Can dy dx be applied to various types of functions?

Yes, "dy dx" can be applied to polynomial, exponential, logarithmic, and trigonometric functions, among others. Each type of function has specific rules for differentiation, which can be systematically applied to understand their behavior better. For example, the power rule allows us to differentiate polynomial functions efficiently.

What does xy 2 mean in mathematical terms?

The expression "xy 2" can be interpreted in different ways depending on the context. It could represent a product of two variables, x and y, followed by the number 2, or it could signify a function defined by these variables. Understanding this notation is crucial for solving equations that involve multiple variables.

How can we combine dy dx and xy 2 in equations?

Combining "dy dx" with "xy 2" often leads to more complex derivatives that require a nuanced understanding of both concepts. For instance, if we have a function defined as z = xy^2, we can apply the product and chain rules to differentiate it with respect to x or y. This process enables us to analyze how changes in one variable affect the others.

Are there practical applications for dy dx xy 2?

Absolutely! The combination of "dy dx" and "xy 2" is prevalent in various fields, including physics for motion analysis, economics for cost functions, and biology for population models. Understanding how these concepts interact can provide deeper insights into real-world scenarios and phenomena.

Read also:

Find Out Josh Hutchersons Age Uncovering The Facts

What are the common challenges faced when working with dy dx xy 2?

One common challenge is managing the complexity of derivatives that involve multiple variables. It often requires a solid understanding of differentiation rules and the ability to apply them correctly. Additionally, interpreting the results of these derivatives can pose challenges, especially in applied contexts.

How can one improve their skills in using dy dx xy 2?

• Practice regularly by solving various problems involving derivatives.
• Study different types of functions and their differentiation rules.
• Engage with online resources, tutorials, or study groups focused on calculus.
• Utilize graphing tools to visualize functions and their derivatives.

In conclusion, understanding "dy dx xy 2" is essential for anyone looking to master calculus and its applications. By exploring the significance of derivatives and their relationship to functions, you can unlock a wealth of knowledge that extends far beyond the classroom. Whether you're a student, educator, or professional, this insight can greatly enhance your mathematical toolkit.